עוד לא נשוי

פתרון חידה (N^3)

טוב, בגלל מיעוט הקוראים/ות, די היה צפוי שלא תהיה תשובה לחידה (אבל, גם כשישראבלוג היה פעיל והיו לי המון קוראים/ות ומגיבים/ות, רובם/ן המכריע לא הצליח לפתור (היו יוצאים/ות מהכלל. היה כאן פעם למשל איזה ילד גאון שהשתתף באולימפיאדות מתמטיקה ופתר כמעט (דגש על כמעט) את כל החידות כאן)), אז "אאלץ" לתת את הפתרונות שלי:

1. שיטה שנסמכת על החידה הריבועית (פחות אלגנטית?): כמו שכתבתי בפוסט הקודם אפשר להשתמש בפתרון החידה הקודמת. כזכור בחידה הריבועית היה צריך לחשב את ריבועי השלמים מ1 עד N עם לולאה אחת, עם פעולות חיבור וללא כפל/חילוק. במקרה הריבועי אפשר פשוט לחשב את ההפרש בין הריבוע של a+1 לריבוע של a ואז להתחיל עם נניח 1 (או 0) ולהגדיל עם ההפרש התורן וכך לקבל ריבועי המספרים. כלומר:

   (a+1)² - a² = a² + 2a + 1 -  a² = 2a + 1 

בכל איטרציה של הלולאה כדי לקבל ריבוע המספר הבא צריך להוסיף פעמיים a ועוד 1.

באופן דומה נחשב ההפרש בין החזקה השלישית של a+1 לחזקה השלישית של a. נקבל:

   (a+1)³ – a³ = a³ + 3a²  + 3a + 1 -  a³ = 3a²  + 3a + 1

את הריבוע של a אנחנו כבר יודעים לחשב, אז העניין פתור. הקוד (בשפה שתיארתי) יכול להיות למשל כזה (A כאן מחזיק את החזקה השניה ו B את השלישית):

Var Int A,B,I,N

Input N

A = 1

B = 1

For I = 1 to N

  PrintLine I," ",B

  B = B + A + A + A + I + I + I + 1

  A = A + I + I + 1

Next I

2. ונעבור לשיטה היותר מעניינת לדעתי (כמו שכתבתי בפוסט קודם, ייתכן שאריתמטית הן שקולות). אני קורא לה "חישוב הפרשים רקורסיבי" שממנה אפשר ליצור (בדרך הפוכה) חיבור כנ"ל. הכוונה תחילה היא למצוא את הערך המספרי של הפרשי החזקות השלישיות. אח"כ לעבור על ההפרשים הללו ולמצוא בהם את ההפרשים וכן הלאה... עד שמגיעים למספר קבוע (או שמזהים תבנית...). מיד אדגים עם טבלה, אבל לפני כן אציין שהמספר הקבוע הזה, 6 במקרה שלנו של חזקה שלישית, הוא העצרת של החזקה (!3 במקרה זה), כלומר אם נעשה חישוב מקביל כזה לחזקות רביעיות נקבל שהקבוע כנ"ל הוא 24 (!4), לחזקות חמישיות 120 (!5) וכן הלאה (וזה לא רמז לפיתרון החידה הבאה (שהזכרתי בפוסט הקודם) בעניין העצרת...).

בטבלה הבאה אפשר לראות, משמאל לימין, את ערכי N, אח"כ את החזקה השלישית של N. אח"כ, בכל תא (לא ריק) של עמודות ההפרש יש את ההפרש בין התא שמשמאל ושורה אחת למטה לתא שמשמאל, למשל ההפרש הראשון בעמודה "הפרש 1" הוא 8 פחות 1, כלומר 7 (אני מניח שאפשר למצוא איזה קשר למשולש פסקל(?)...):

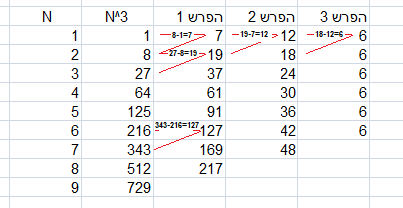
אפשר לראות ש"הפרש 3" הוא תמיד 6 ע"י:

כזכור ההפרש בין a+1 בשלישית ל a בשלישית היה:

3a²  + 3a + 1 זה בעצם "הפרש 1",

אפשר לחשב את "הפרש 2" ע"י הצבה של a+1 בביטוי הקודם במקום a ולהחסיר מזה את הביטוי הנ"ל, כלומר:

3(a+1)²  + 3(a+1) + 1 - 3a²  - 3a – 1

וזה נותן:

6a + 6

עכשיו אפשר לחשב את "הפרש 3" ע"י הצבה בדומה של המספר העוקב והחסרה:

6(a+1) + 6 – 6a - 6 = 6a + 6 + 6 - 6a – 6 = 6

לכן השיטה היותר "חסכונית" בחישוב (פחות פעולות חיבור) יכולה להיות כזו:

Var Int A,B,C,I,N

Input N

A = 0

B = 1

C = 6

For I = 1 to N

  A = A + B

  B = B + C

  C = C + 6

  PrintLine I," ",A

Next I

שנה טובה

בהזדמנות זו (למרות שאני כמובן יהודי ולא נוצרי) אאחל שנה אזרחית חדשה טובה. אם שמתם/ן לב בשנה הזו יש הרבה "2"... כמו שמציינים את "יום הרווקים הסיני" ב11.11 בגלל ה"1" (מייצג רווקים), כך אולי השנה הזו תביא איתה זוגיות... אינשאללה.

כדרכי בקודש אני שם כאן את הציור של מה שאני מחפש חיצונית בבת-זוג. אז הנה דוגמא לבחורה (דימיונית) שהיא בערך הטעם שלי, לפחות כללית עם דגש על מבנה גוף:

כאמור זה תיאור כללי (כלומר יש 'דרגות חופש' לטעם שלי ואין מודל אחד ויחיד) של מה שאני מחפש חיצונית בבת-זוג ומה מושך אותי. אני תמיד מדגיש שאני מחפש מישהי אך ורק למטרה רצינית (אז... אני חוזר על זה שוב). על הצדדים האחרים (שלא פחות חשובים) של מה שאני מחפש בבת-זוג כתבתי בקישור *הזה* . עלי כתבתי בקישור *הזה*  (שני הנ"ל מקושרים כאן בבלוג ברשימות מצד ימין). האי-מייל שלי (לבחורות מתאימות, או מי מטעמן) לפניות הוא [email protected].